On the Relaxation of Some Types of Dirichlet Minimum Problems for Unbounded Functionals
Abstract
In this paper, considered a Borel function g on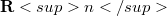 
taking its values in ![[0,+∈fty]](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/58a7e463b0398b5e001377bb1bf80ce4.png)
, verifying some weak hypothesis of continuity, such that 
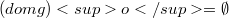and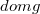 
is convex, we obtain an integral representation result for the lower semicontinuous envelope in the 
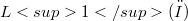- topology of the integral functional 
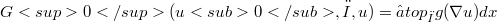, where(Error rendering LaTeX formula) only on suitable pin is of the boundary of 
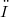that lie, for example, on affine spaces orthogonal to 
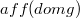, for boundary values 
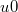satisfying suitable compatibility conditions and 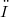is geometrically well situated respect to 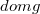. Then we apply this result to Dirichlet nunimum problems.
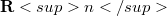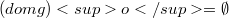taking its values in , verifying some weak hypothesis of continuity, such that and 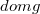is convex, we obtain an integral representation result for the lower semicontinuous envelope in the 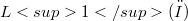- topology of the integral functional 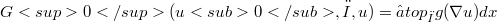, where(Error rendering LaTeX formula) only on suitable pin is of the boundary of 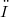that lie, for example, on affine spaces orthogonal to 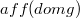, for boundary values 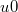satisfying suitable compatibility conditions and 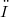is geometrically well situated respect to 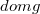. Then we apply this result to Dirichlet nunimum problems.DOI Code:
10.1285/i15900932v19n2p231
Classification:
49J45
Full Text: PDF
