A note on embeddings of projective spaces
Abstract
Let 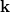 and
and 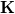 be commutative fields, and
be commutative fields, and 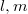 integers with
integers with 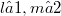 . Suppose that there exists an embedding
. Suppose that there exists an embedding 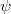 of
of 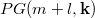 to
to 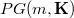 , then we have
, then we have 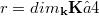 and
and ![m ≥ ≤ft [{3l}\over{r-3}\right] - 1](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/d30734a9663178578a33592f8d9a1617.png) . Conversely, there exists an embedding
. Conversely, there exists an embedding 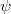 of
of 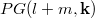 to
to 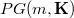 if
if ![m ≥ ≤ft [{3l}\over{r-3}\right] - 1](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/d30734a9663178578a33592f8d9a1617.png) and if (1)
and if (1) 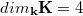 , or (2)
, or (2) 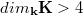 and
and 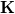 is a cyclic extension of
is a cyclic extension of 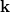 with some additional conditions on l and r.
with some additional conditions on l and r.
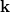 and
and 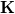 be commutative fields, and
be commutative fields, and 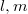 integers with
integers with 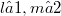 . Suppose that there exists an embedding
. Suppose that there exists an embedding 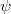 of
of 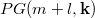 to
to 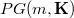 , then we have
, then we have 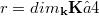 and
and ![m ≥ ≤ft [{3l}\over{r-3}\right] - 1](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/d30734a9663178578a33592f8d9a1617.png) . Conversely, there exists an embedding
. Conversely, there exists an embedding 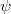 of
of 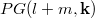 to
to 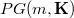 if
if ![m ≥ ≤ft [{3l}\over{r-3}\right] - 1](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/d30734a9663178578a33592f8d9a1617.png) and if (1)
and if (1) 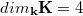 , or (2)
, or (2) 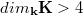 and
and 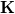 is a cyclic extension of
is a cyclic extension of 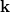 with some additional conditions on l and r.
with some additional conditions on l and r.DOI Code:
10.1285/i15900932v19n2p285
Full Text: PDF


