Dual parallelisms
Abstract
Assume that 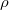 is a parallelism in
is a parallelism in 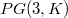 , for
, for 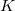 a field, that admits a collineation group
a field, that admits a collineation group 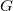 that fixes one spread
that fixes one spread 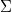 and acts transitively on the remaining spreads of
and acts transitively on the remaining spreads of 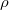 . If
. If 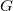 contains suitable central collineations of
contains suitable central collineations of 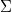 then it is shown that the dual parallelism is a parallelism that can never be isomorphic to the original. The results show that the Johnson parallelisms of Hall or Knuth type, the Johnson-Pomareda parallelisms of type
then it is shown that the dual parallelism is a parallelism that can never be isomorphic to the original. The results show that the Johnson parallelisms of Hall or Knuth type, the Johnson-Pomareda parallelisms of type 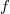 and all of the "derived" parallelisms produce dual parallelisms which are parallelisms but are nonisomorphic to the original parallelism.
and all of the "derived" parallelisms produce dual parallelisms which are parallelisms but are nonisomorphic to the original parallelism.
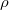 is a parallelism in
is a parallelism in 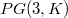 , for
, for 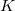 a field, that admits a collineation group
a field, that admits a collineation group 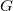 that fixes one spread
that fixes one spread 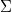 and acts transitively on the remaining spreads of
and acts transitively on the remaining spreads of 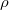 . If
. If 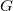 contains suitable central collineations of
contains suitable central collineations of 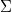 then it is shown that the dual parallelism is a parallelism that can never be isomorphic to the original. The results show that the Johnson parallelisms of Hall or Knuth type, the Johnson-Pomareda parallelisms of type
then it is shown that the dual parallelism is a parallelism that can never be isomorphic to the original. The results show that the Johnson parallelisms of Hall or Knuth type, the Johnson-Pomareda parallelisms of type 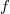 and all of the "derived" parallelisms produce dual parallelisms which are parallelisms but are nonisomorphic to the original parallelism.
and all of the "derived" parallelisms produce dual parallelisms which are parallelisms but are nonisomorphic to the original parallelism.DOI Code:
10.1285/i15900932v21n1p137
Keywords:
Parallelisms; Dual parallelisms
Classification:
51E23; 51A40
Full Text: PDF


