Generalizations of Fibonacci and Lucas sequences
Abstract
In this paper, we consider the Hecke groups 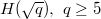 prime number, and we find an interesting number sequence whichis denoted by
prime number, and we find an interesting number sequence whichis denoted by 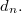 For
For 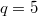 , we get
, we get 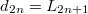 and
and 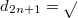 where
where 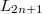 is
is 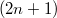 th Lucas number and
th Lucas number and 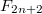 is
is 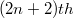 Fibonacci number. From this sequence, we obtain two new sequenceswhich are, in a sense, generalizations of Fibonacci and Lucas sequences.
Fibonacci number. From this sequence, we obtain two new sequenceswhich are, in a sense, generalizations of Fibonacci and Lucas sequences.
DOI Code:
10.1285/i15900932v21n1p113
Keywords:
Hecke groups; Fibonacci numbers; Lucas numbers
Classification:
11B39; 20H10
Full Text: PDF


