An Eightfold Littlewood-Richardson Theorem
Abstract
Based on a generalized ordering 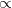 on a set
on a set 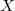 , Schensted's insertion mapping is defined on the set of words
, Schensted's insertion mapping is defined on the set of words 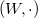 over the ordered alphabet
over the ordered alphabet 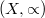 . In this general framework, a transparent approach to various versions of the Robinson-Schensted correspondence and of invariant properties originally due to Schützenberger, Knuth, White e.a. is obtained. Furthermore, eight combinatorial descriptions of the Littlewood-Richardson coefficients are obtained simultaneously, and direct bijections between the corresponding sets, including the bijection of Hanlon and Sundaram. Some of these descriptions may be translated into identities of skew Schur functions discovered by Aitken and Berenstein/Zelevinsky.
. In this general framework, a transparent approach to various versions of the Robinson-Schensted correspondence and of invariant properties originally due to Schützenberger, Knuth, White e.a. is obtained. Furthermore, eight combinatorial descriptions of the Littlewood-Richardson coefficients are obtained simultaneously, and direct bijections between the corresponding sets, including the bijection of Hanlon and Sundaram. Some of these descriptions may be translated into identities of skew Schur functions discovered by Aitken and Berenstein/Zelevinsky.
DOI Code:
10.1285/i15900932v21n1p1
Keywords:
Schensted insertion; Generalized ordering; Tableau
Classification:
20C30; 05E10
Full Text: PDF


