Lie symmetries of differential equations:direct and inverse problems
Abstract
This paper reviews some relevant problems arising within the context of Lie group analysis of differential equations either in the direct approach or in the inverse one.For what concerns the direct approach, there are considered two results,the first related to the reduction through an invertible point transformation of a system of PDE's to an equivalent autonomous form, and the second related to the reduction of a nonlinear first order system of PDE's to linear form.Two applications of the results are given.The Navier-Stokes- Fourier model equations for a viscous and heat conducting monatomic gas in a rotating frame are mapped in two different autonomous forms,and some explicit exact solutions are determined.
Moreover,the first order system corresponding to the most general second order completely exceptional equation in 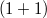 dimensions (which is a Monge-Ampère equation) is reduced to linear form. Finally, within the context of the inverse approach of Lie group analysis, there is introduced the concept of Lie remarkable systems and it is shown that second order Monge-Ampère equations and the third order Monge-Ampère equation in
dimensions (which is a Monge-Ampère equation) is reduced to linear form. Finally, within the context of the inverse approach of Lie group analysis, there is introduced the concept of Lie remarkable systems and it is shown that second order Monge-Ampère equations and the third order Monge-Ampère equation in 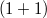 dimensions are Lie remarkable.
dimensions are Lie remarkable.
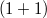 dimensions (which is a Monge-Ampère equation) is reduced to linear form. Finally, within the context of the inverse approach of Lie group analysis, there is introduced the concept of Lie remarkable systems and it is shown that second order Monge-Ampère equations and the third order Monge-Ampère equation in
dimensions (which is a Monge-Ampère equation) is reduced to linear form. Finally, within the context of the inverse approach of Lie group analysis, there is introduced the concept of Lie remarkable systems and it is shown that second order Monge-Ampère equations and the third order Monge-Ampère equation in 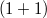 dimensions are Lie remarkable.
dimensions are Lie remarkable.DOI Code:
10.1285/i15900932v23n2p195
Keywords:
Lie point symmetries; Autonomous differential equations; Linearizable differential equations; Completely exceptional equations; Lie remarkable equations
Classification:
58J70; 35L75
Full Text: PDF


