Higher order valued reduction theorems for general linear connections

Abstract

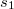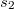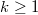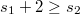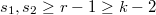The reduction theorems for general linear and classical connections are  generalized for operators with values in higher order gauge-natural bundles.  We prove that natural operators depending on the -jets of classical  connections, on the -jets of general linear connections and on the  -jets of tensor fields with values in gauge-natural bundles of order , , , can be factorized through the  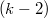-jets of both connections, the 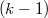-jets of the tensor fields and  sufficiently high covariant differentials of the curvature tensors and the  tensor fields.