Canonical decompositions induced by 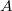 -contractions
-contractions
Abstract
The classical Nagy-Foia\c s-Langer decomposition of an ordinary contraction is generalized in the context of the operators 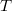 on a complex Hilbert space
on a complex Hilbert space 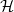 which, relative to a positive operator
which, relative to a positive operator 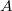 on
on 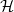 , satisfy the inequality
, satisfy the inequality 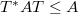 . As a consequence, a version of the classical von Neumann-Wold decomposition for isometries is derived in this context. Also one shows that, if
. As a consequence, a version of the classical von Neumann-Wold decomposition for isometries is derived in this context. Also one shows that, if 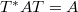 and
and 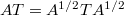 , then the decomposition of
, then the decomposition of 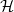 in normal part and pure part relative to
in normal part and pure part relative to 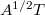 is just a von Neumann-Wold type decomposition for
is just a von Neumann-Wold type decomposition for 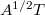 , which can be completely described. As applications, some facts on the quasi-isometries recently studied in [4], [5], are obtained.
, which can be completely described. As applications, some facts on the quasi-isometries recently studied in [4], [5], are obtained.
DOI Code:
10.1285/i15900932v28n2p187
Keywords:
A-contraction; A-isometry; quasi-isometry; von Neumann-Wold decomposition
Classification:
47A15; 47A63; 47B20
Full Text: PDF


