Best Simultaneous 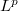   Approximation in the "Sum" Norm

doi:10.1285/i15900932v28n2p153

Best Simultaneous $L^p$ Approximation in the "Sum" Norm

H´ector H. Cuenya, Claudia N. Rodriguez

Abstract

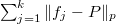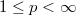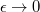In this paper we consider best simultaneous approximation byalgebraic polynomials respect to the norm $\sum_{j=1}^k\|f_j-P\|_p$ , $1\le p<\infty$ . We prove an interpolation propertyof the best simultaneous approximations and we study the structureof the set of cluster points of the best simultaneousapproximations on the interval $[-\epsilon,\epsilon],$ as $\epsilon \to 0$ .