On exact locally conformally Kähler manifolds
Abstract
In this article, we explore a distinguished class of complex manifolds known as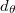 
-exact locally conformally Kähler (LCK) manifolds. These manifolds are characterized by the property that their fundamental 2-form 
can be expressed as 
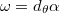, where 
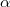is a 1-form on 
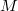and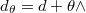 
. We establish a key result: if the 1-form 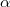is holomorphic, then the Morse-Novikov cohomology 
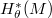vanishes. Furthermore, we provide sufficient conditions under which a 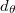-exact LCK manifold admits a Vaisman structure. This work deepens the understanding of the interplay between geometric structures, cohomological properties, and special classes of LCK manifolds.
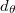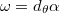-exact locally conformally Kähler (LCK) manifolds. These manifolds are characterized by the property that their fundamental 2-form can be expressed as , where 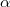is a 1-form on 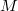and 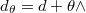. We establish a key result: if the 1-form 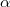is holomorphic, then the Morse-Novikov cohomology 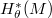vanishes. Furthermore, we provide sufficient conditions under which a 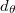-exact LCK manifold admits a Vaisman structure. This work deepens the understanding of the interplay between geometric structures, cohomological properties, and special classes of LCK manifolds.Keywords:
Locally conformally Kähler manifolds; $\(d_\theta\)$-exact LCK manifolds; Lee form; Morse-Novikov cohomology; Vaisman manifolds
Full Text: PDF
