Ideals as Generalized Prime Ideal Factorization of Submodules
Abstract
For a submodule 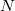 of an
of an 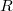 -module
-module 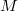 , a unique product of prime ideals in
, a unique product of prime ideals in 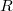 is assigned, which is called the generalized prime ideal factorization of
is assigned, which is called the generalized prime ideal factorization of 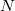 in
in 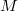 , and denoted as
, and denoted as 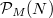 . But for a product of prime ideals
. But for a product of prime ideals 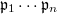 in
in 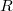 and an
and an 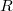 -module
-module 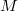 , there may not exist a submodule
, there may not exist a submodule 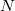 in
in 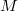 with
with 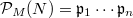 . In this article, for an arbitrary product of prime ideals
. In this article, for an arbitrary product of prime ideals 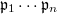 and a module
and a module 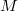 , we find conditions for the existence of submodules in
, we find conditions for the existence of submodules in 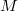 having
having 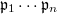 as their generalized prime ideal factorization
as their generalized prime ideal factorization
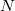 of an
of an 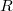 -module
-module 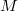 , a unique product of prime ideals in
, a unique product of prime ideals in 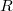 is assigned, which is called the generalized prime ideal factorization of
is assigned, which is called the generalized prime ideal factorization of 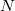 in
in 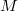 , and denoted as
, and denoted as 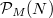 . But for a product of prime ideals
. But for a product of prime ideals 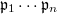 in
in 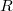 and an
and an 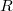 -module
-module 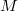 , there may not exist a submodule
, there may not exist a submodule 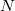 in
in 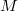 with
with 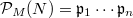 . In this article, for an arbitrary product of prime ideals
. In this article, for an arbitrary product of prime ideals 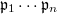 and a module
and a module 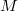 , we find conditions for the existence of submodules in
, we find conditions for the existence of submodules in 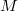 having
having 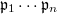 as their generalized prime ideal factorization
as their generalized prime ideal factorizationDOI Code:
10.1285/i15900932v44n1p13
Keywords:
prime submodule; prime filtration; Noetherian ring; prime ideal factorization; regular prime extension filtration
Full Text: PDF


