Recognizing Euclidean Space Forms with Minimal Fundamental Tetrahedra
Abstract
We completely recognize the topological structure of the ten compact euclidean space forms with special minimal tetrahedra, constructed by face pairings in nice papers of Molnár [8-9]. From these polyhedral descriptions we derive special presentations with two generators for the fundamental groups of the considered manifolds. Our proofs also show that such group presentations completely characterize the euclidean space forms among closed connected 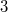 -manifolds. The results have also didactical importance.
-manifolds. The results have also didactical importance.
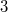 -manifolds. The results have also didactical importance.
-manifolds. The results have also didactical importance.DOI Code:
10.1285/i15900932v41n2p85
Keywords:
Finitely generated group; spine; Seifert manifold; torus bundle; space form; polyhedral representation; Schlegel diagram
Full Text: PDF


