The Erd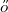 s-Faber-Lovász Conjecture revisited
s-Faber-Lovász Conjecture revisited
Abstract
The Erd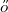 s-Faber-Lovász Conjecture, posed in 1972, states that if a graph
s-Faber-Lovász Conjecture, posed in 1972, states that if a graph  is the union of
is the union of  cliques of order
cliques of order  (referred to as defining
(referred to as defining  -cliques) such that two cliques can share at most one vertex, then the vertices of
-cliques) such that two cliques can share at most one vertex, then the vertices of  can be properly coloured using
can be properly coloured using  colours. Although still open after almost 50 years, it can be easily shown that the conjecture is true when every shared vertex belongs to exactly two defining
colours. Although still open after almost 50 years, it can be easily shown that the conjecture is true when every shared vertex belongs to exactly two defining  -cliques. We here provide a quick and easy algorithm to colour the vertices of
-cliques. We here provide a quick and easy algorithm to colour the vertices of  in this case, and discuss connections with clique-decompositions and edge-colourings of graphs.
in this case, and discuss connections with clique-decompositions and edge-colourings of graphs.
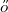 s-Faber-Lovász Conjecture, posed in 1972, states that if a graph
s-Faber-Lovász Conjecture, posed in 1972, states that if a graph  is the union of
is the union of  cliques of order
cliques of order  (referred to as defining
(referred to as defining  -cliques) such that two cliques can share at most one vertex, then the vertices of
-cliques) such that two cliques can share at most one vertex, then the vertices of  can be properly coloured using
can be properly coloured using  colours. Although still open after almost 50 years, it can be easily shown that the conjecture is true when every shared vertex belongs to exactly two defining
colours. Although still open after almost 50 years, it can be easily shown that the conjecture is true when every shared vertex belongs to exactly two defining  -cliques. We here provide a quick and easy algorithm to colour the vertices of
-cliques. We here provide a quick and easy algorithm to colour the vertices of  in this case, and discuss connections with clique-decompositions and edge-colourings of graphs.
in this case, and discuss connections with clique-decompositions and edge-colourings of graphs.DOI Code:
10.1285/i15900932v41n2p1
Keywords:
Erdös-Faber-Lovász Conjecture; chromatic number; clique-decomposition; edge-colouring
Full Text: PDF


