Frame measures for infinitely many measures
Abstract
For every frame spectral measure 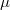 , there exists a discrete measure
, there exists a discrete measure  as a frame measure. If
as a frame measure. If 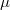 is not a frame spectral measure, then there is not any general statement about the existence of frame measures
is not a frame spectral measure, then there is not any general statement about the existence of frame measures  for
for 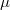 . This motivated us to examine Bessel and frame measures. We construct infinitely many measures
. This motivated us to examine Bessel and frame measures. We construct infinitely many measures 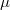 which admit frame measures
which admit frame measures  , and we show that there exist infinitely many frame spectral measures
, and we show that there exist infinitely many frame spectral measures 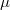 such that besides having a discrete frame measure, they admit continuous frame measures too.
such that besides having a discrete frame measure, they admit continuous frame measures too.
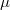 , there exists a discrete measure
, there exists a discrete measure  as a frame measure. If
as a frame measure. If 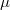 is not a frame spectral measure, then there is not any general statement about the existence of frame measures
is not a frame spectral measure, then there is not any general statement about the existence of frame measures  for
for 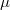 . This motivated us to examine Bessel and frame measures. We construct infinitely many measures
. This motivated us to examine Bessel and frame measures. We construct infinitely many measures 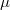 which admit frame measures
which admit frame measures  , and we show that there exist infinitely many frame spectral measures
, and we show that there exist infinitely many frame spectral measures 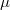 such that besides having a discrete frame measure, they admit continuous frame measures too.
such that besides having a discrete frame measure, they admit continuous frame measures too.DOI Code:
10.1285/i15900932v40n1p115
Keywords:
Fourier frame; Plancherel theorem; spectral measure; frame measure; Bessel measure
Full Text: PDF


