Homogeneous geodesics and g.o. manifolds
Abstract
Let 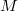 be a homogeneous pseudo-Riemannian manifold, affine manifold, or Finsler space. A homogeneous geodesic is an orbit of a
be a homogeneous pseudo-Riemannian manifold, affine manifold, or Finsler space. A homogeneous geodesic is an orbit of a 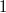 -parameter group of isometries, respectively, of affine diffeomorphisms. A homogeneous manifold is called a g.o. manifold if all geodesics are homogeneous. Homogeneous geodesics were studied first in Riemannian manifolds using the algebraic tool called geodesic lemma. This was generalized for Finsler spaces and also for pseudo-Riemannian reductive manifolds, where new phenomena appear. The non-reductive homogeneous pseudo-Riemannian manifolds can be studied in the broader context of homogeneous affine manifolds using the more fundamental affine method based on Killing vector fields. In Finsler geometry, both the algebraic approach to reductive spaces and the affine approach can be used. The present paper is a survey on the interesting phenomena and examples related with the existence of homogeneous geodesics and with g.o. manifolds in Riemannian, pseudo-Riemannian, affine and Finsler geometry.
-parameter group of isometries, respectively, of affine diffeomorphisms. A homogeneous manifold is called a g.o. manifold if all geodesics are homogeneous. Homogeneous geodesics were studied first in Riemannian manifolds using the algebraic tool called geodesic lemma. This was generalized for Finsler spaces and also for pseudo-Riemannian reductive manifolds, where new phenomena appear. The non-reductive homogeneous pseudo-Riemannian manifolds can be studied in the broader context of homogeneous affine manifolds using the more fundamental affine method based on Killing vector fields. In Finsler geometry, both the algebraic approach to reductive spaces and the affine approach can be used. The present paper is a survey on the interesting phenomena and examples related with the existence of homogeneous geodesics and with g.o. manifolds in Riemannian, pseudo-Riemannian, affine and Finsler geometry.
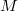 be a homogeneous pseudo-Riemannian manifold, affine manifold, or Finsler space. A homogeneous geodesic is an orbit of a
be a homogeneous pseudo-Riemannian manifold, affine manifold, or Finsler space. A homogeneous geodesic is an orbit of a 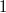 -parameter group of isometries, respectively, of affine diffeomorphisms. A homogeneous manifold is called a g.o. manifold if all geodesics are homogeneous. Homogeneous geodesics were studied first in Riemannian manifolds using the algebraic tool called geodesic lemma. This was generalized for Finsler spaces and also for pseudo-Riemannian reductive manifolds, where new phenomena appear. The non-reductive homogeneous pseudo-Riemannian manifolds can be studied in the broader context of homogeneous affine manifolds using the more fundamental affine method based on Killing vector fields. In Finsler geometry, both the algebraic approach to reductive spaces and the affine approach can be used. The present paper is a survey on the interesting phenomena and examples related with the existence of homogeneous geodesics and with g.o. manifolds in Riemannian, pseudo-Riemannian, affine and Finsler geometry.
-parameter group of isometries, respectively, of affine diffeomorphisms. A homogeneous manifold is called a g.o. manifold if all geodesics are homogeneous. Homogeneous geodesics were studied first in Riemannian manifolds using the algebraic tool called geodesic lemma. This was generalized for Finsler spaces and also for pseudo-Riemannian reductive manifolds, where new phenomena appear. The non-reductive homogeneous pseudo-Riemannian manifolds can be studied in the broader context of homogeneous affine manifolds using the more fundamental affine method based on Killing vector fields. In Finsler geometry, both the algebraic approach to reductive spaces and the affine approach can be used. The present paper is a survey on the interesting phenomena and examples related with the existence of homogeneous geodesics and with g.o. manifolds in Riemannian, pseudo-Riemannian, affine and Finsler geometry.DOI Code:
10.1285/i15900932v38n1p1
Keywords:
Homogeneous manifold; homogeneous geodesic; Killing vector field
Full Text: PDF


