On Mutually Orthogonal Disjoint Copies of Graph Squares
Abstract
A family of decompositions 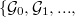 of a complete bipartite graph
of a complete bipartite graph 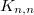 is a set of
is a set of 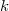 \textit{mutually orthogonal graph squares}
\textit{mutually orthogonal graph squares} 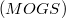 if
if 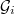 and
and 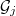 \ are orthogonal for all
\ are orthogonal for all 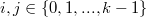 and
and  . For any subgraph
. For any subgraph  of
of 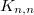 with
with  edges,
edges, 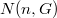 denotes the maximum number
denotes the maximum number 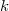 in a largest possible set(Error rendering LaTeX formula) of
in a largest possible set(Error rendering LaTeX formula) of 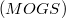 of
of 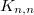 by
by  . Our objective of this paper is to compute
. Our objective of this paper is to compute 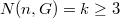 where
where  represents disjoint copies of certain subgraphs of
represents disjoint copies of certain subgraphs of 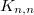 .
.
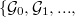 of a complete bipartite graph
of a complete bipartite graph 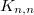 is a set of
is a set of 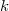 \textit{mutually orthogonal graph squares}
\textit{mutually orthogonal graph squares} 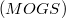 if
if 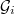 and
and 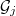 \ are orthogonal for all
\ are orthogonal for all 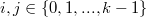 and
and  . For any subgraph
. For any subgraph  of
of 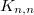 with
with  edges,
edges, 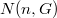 denotes the maximum number
denotes the maximum number 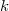 in a largest possible set(Error rendering LaTeX formula) of
in a largest possible set(Error rendering LaTeX formula) of  of
of 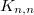 by
by  . Our objective of this paper is to compute
. Our objective of this paper is to compute 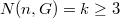 where
where  represents disjoint copies of certain subgraphs of
represents disjoint copies of certain subgraphs of 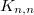 .
.DOI Code:
10.1285/i15900932v36n2p89
Keywords:
Orthogonal graph squares; Orthogonal double cover; Mutually orthogonal Latin squares
Full Text: PDF


