Characterization of ultradifferentiable test functions defined by weight matrices in terms of their Fourier Transform
Abstract
We prove that functions with compact support in non-quasianalytic classes 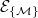 of Roumieu-type and
of Roumieu-type and 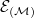 of Beurling-type defined by a weight matrix
of Beurling-type defined by a weight matrix 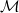 with some mild regularity conditions can be characterized by the decay properties of their Fourier transform. For this we introduce the abstract technique of constructing from
with some mild regularity conditions can be characterized by the decay properties of their Fourier transform. For this we introduce the abstract technique of constructing from 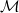 multi-index matrices and associated function spaces. We study the behaviour of this construction in detail and characterize its stability. Moreover non-quasianalyticity of the classes mathcal{E}_{\{\mathcal{M}\}}
multi-index matrices and associated function spaces. We study the behaviour of this construction in detail and characterize its stability. Moreover non-quasianalyticity of the classes mathcal{E}_{\{\mathcal{M}\}}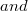 \mathcal{E}_{(\mathcal{M})}$ is characterized.
\mathcal{E}_{(\mathcal{M})}$ is characterized.
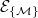 of Roumieu-type and
of Roumieu-type and 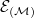 of Beurling-type defined by a weight matrix
of Beurling-type defined by a weight matrix 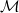 with some mild regularity conditions can be characterized by the decay properties of their Fourier transform. For this we introduce the abstract technique of constructing from
with some mild regularity conditions can be characterized by the decay properties of their Fourier transform. For this we introduce the abstract technique of constructing from 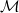 multi-index matrices and associated function spaces. We study the behaviour of this construction in detail and characterize its stability. Moreover non-quasianalyticity of the classes mathcal{E}_{\{\mathcal{M}\}}
multi-index matrices and associated function spaces. We study the behaviour of this construction in detail and characterize its stability. Moreover non-quasianalyticity of the classes mathcal{E}_{\{\mathcal{M}\}}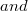 \mathcal{E}_{(\mathcal{M})}$ is characterized.
\mathcal{E}_{(\mathcal{M})}$ is characterized.DOI Code:
10.1285/i15900932v36n2p1
Keywords:
Ultradifferentiable functions; non-quasianalyticity; Fourier transform
Full Text: PDF


