Harmonic maps into real hyperbolic space
Abstract
In [2,4,5,6,7 ] Calabi, Borbosa and Chern showed that there is a one-to-one correspondence between arbitrary pairs of full isotropic (terminology as in [8]) harmonic maps 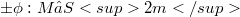 from a Riemann surface to Euclidean sphere and full totally isotropic holomorphic maps
from a Riemann surface to Euclidean sphere and full totally isotropic holomorphic maps 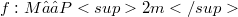 from the surface to complex projective space.In this paper we show, very explicity, how to construct a similar one-to-one correspondence when
from the surface to complex projective space.In this paper we show, very explicity, how to construct a similar one-to-one correspondence when 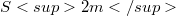 is replaced by real hyperbolic space
is replaced by real hyperbolic space 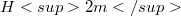 with its standard metric. We get over a difficulty encountered by Barbosa of dealing with the zeros of certain wedge product by a technique adapted from [8].(The case of indefinite complex hyperbolic and projective spaces will be considered in a separate paper).
with its standard metric. We get over a difficulty encountered by Barbosa of dealing with the zeros of certain wedge product by a technique adapted from [8].(The case of indefinite complex hyperbolic and projective spaces will be considered in a separate paper).
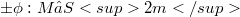 from a Riemann surface to Euclidean sphere and full totally isotropic holomorphic maps
from a Riemann surface to Euclidean sphere and full totally isotropic holomorphic maps 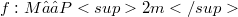 from the surface to complex projective space.In this paper we show, very explicity, how to construct a similar one-to-one correspondence when
from the surface to complex projective space.In this paper we show, very explicity, how to construct a similar one-to-one correspondence when 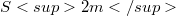 is replaced by real hyperbolic space
is replaced by real hyperbolic space 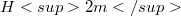 with its standard metric. We get over a difficulty encountered by Barbosa of dealing with the zeros of certain wedge product by a technique adapted from [8].(The case of indefinite complex hyperbolic and projective spaces will be considered in a separate paper).
with its standard metric. We get over a difficulty encountered by Barbosa of dealing with the zeros of certain wedge product by a technique adapted from [8].(The case of indefinite complex hyperbolic and projective spaces will be considered in a separate paper).DOI Code:
10.1285/i15900932v3n1p29
Full Text: PDF


