Questioni di suriettività di un morfismo canonico tra due complessi approssimati
Abstract
In this paper, we introduce the concept of i-couple for two ideals, 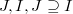 , in a local noetherian ring
, in a local noetherian ring 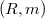 .This concept is expressed in terms of the structure of
.This concept is expressed in terms of the structure of 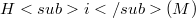 (where M is an approximation complex for the double Koszul complex L associated to the system of generators of J), and it generalizes the idea of (d,i)-sequence introduce in [M-R].We study the relationship between the following properties: 1)
(where M is an approximation complex for the double Koszul complex L associated to the system of generators of J), and it generalizes the idea of (d,i)-sequence introduce in [M-R].We study the relationship between the following properties: 1) 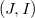 is an i- couple of ideals in R; 2)
is an i- couple of ideals in R; 2) 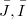 is an i- couple of ideals in
is an i- couple of ideals in 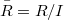 , more generally, in
, more generally, in 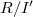 ,
, 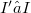 .So we get some sufficient conditions for the "ascendent" and "descendent" properties of the i –couple.In particular, we study the surjectivity of the natural morphism(Error rendering LaTeX formula), since the surjectivity of
.So we get some sufficient conditions for the "ascendent" and "descendent" properties of the i –couple.In particular, we study the surjectivity of the natural morphism(Error rendering LaTeX formula), since the surjectivity of 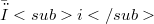 is a sufficient condition for the "descendent" property of the i - ouple from R to
is a sufficient condition for the "descendent" property of the i - ouple from R to 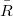 .
.
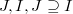 , in a local noetherian ring
, in a local noetherian ring 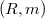 .This concept is expressed in terms of the structure of
.This concept is expressed in terms of the structure of 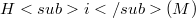 (where M is an approximation complex for the double Koszul complex L associated to the system of generators of J), and it generalizes the idea of (d,i)-sequence introduce in [M-R].We study the relationship between the following properties: 1)
(where M is an approximation complex for the double Koszul complex L associated to the system of generators of J), and it generalizes the idea of (d,i)-sequence introduce in [M-R].We study the relationship between the following properties: 1) 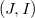 is an i- couple of ideals in R; 2)
is an i- couple of ideals in R; 2) 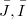 is an i- couple of ideals in
is an i- couple of ideals in 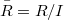 , more generally, in
, more generally, in 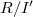 ,
, 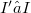 .So we get some sufficient conditions for the "ascendent" and "descendent" properties of the i –couple.In particular, we study the surjectivity of the natural morphism(Error rendering LaTeX formula), since the surjectivity of
.So we get some sufficient conditions for the "ascendent" and "descendent" properties of the i –couple.In particular, we study the surjectivity of the natural morphism(Error rendering LaTeX formula), since the surjectivity of 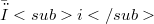 is a sufficient condition for the "descendent" property of the i - ouple from R to
is a sufficient condition for the "descendent" property of the i - ouple from R to 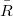 .
.DOI Code:
10.1285/i15900932v6n1p61
Full Text: PDF


