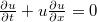A note on a family of distributional products important in the applications
Abstract
We define a family of products of a distribution 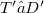 by a distribution
by a distribution 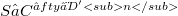 where
where 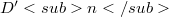 means the space of distributions with support nowhere dense. Each product depends on the choice of a group G of unimodular transformations and a function
means the space of distributions with support nowhere dense. Each product depends on the choice of a group G of unimodular transformations and a function 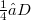 with
with 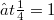 which is G-invariant.These products are consistent with the usual product of a distribution by a
which is G-invariant.These products are consistent with the usual product of a distribution by a 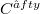 - function, their outcome distributive, and verify also the usual law of the derivate of a product together with being invariant by translation and all transformations in G. A sufficient condition for associativity is given. Simple physical interpretations of the products
- function, their outcome distributive, and verify also the usual law of the derivate of a product together with being invariant by translation and all transformations in G. A sufficient condition for associativity is given. Simple physical interpretations of the products 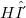 and
and 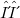 , where H is the Heaviside function and δ is the Dirac’s measure, are considered. In particular we discuss certain shock wave solution of the differential equation
, where H is the Heaviside function and δ is the Dirac’s measure, are considered. In particular we discuss certain shock wave solution of the differential equation
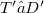 by a distribution
by a distribution 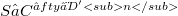 where
where 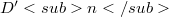 means the space of distributions with support nowhere dense. Each product depends on the choice of a group G of unimodular transformations and a function
means the space of distributions with support nowhere dense. Each product depends on the choice of a group G of unimodular transformations and a function 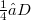 with
with 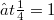 which is G-invariant.These products are consistent with the usual product of a distribution by a
which is G-invariant.These products are consistent with the usual product of a distribution by a 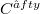 - function, their outcome distributive, and verify also the usual law of the derivate of a product together with being invariant by translation and all transformations in G. A sufficient condition for associativity is given. Simple physical interpretations of the products
- function, their outcome distributive, and verify also the usual law of the derivate of a product together with being invariant by translation and all transformations in G. A sufficient condition for associativity is given. Simple physical interpretations of the products 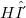 and
and 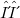 , where H is the Heaviside function and δ is the Dirac’s measure, are considered. In particular we discuss certain shock wave solution of the differential equation
, where H is the Heaviside function and δ is the Dirac’s measure, are considered. In particular we discuss certain shock wave solution of the differential equation .
DOI Code:
10.1285/i15900932v7n2p151
Full Text: PDF