Generalized Jacobi identities
Abstract
In any Lie ring 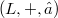 , the following equations hold for arbitrary elements
, the following equations hold for arbitrary elements 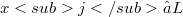 :(Error rendering LaTeX formula) (Error rendering LaTeX formula) In [4,(9a)], Wever already notes that one also has (Error rendering LaTeX formula) and proves some further similar assertions in the same paper [4,Hilfssatz 1]. The aim of this note is, roughly spoken, to determine all relations of this kind.As the relations in question shall hold in any Lie ring, we consider them as relations of free generators
:(Error rendering LaTeX formula) (Error rendering LaTeX formula) In [4,(9a)], Wever already notes that one also has (Error rendering LaTeX formula) and proves some further similar assertions in the same paper [4,Hilfssatz 1]. The aim of this note is, roughly spoken, to determine all relations of this kind.As the relations in question shall hold in any Lie ring, we consider them as relations of free generators 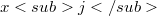 of a free Lie algebra over an arbitrary commutative ring R with identity 1.Then it turns out that in order to determine all relations of the type mentioned above one has to describe a certain right ideal of the group ring of some symmetric group over R. In fact, our main result will solve the problem by exhibiting an R-basis of this «right ideal of generalized Jacobi identities». Our approach makes use of Witt’s theorem [l,2.3.3] on the embedding of a free Lie algebra L in a free associative algebra A. We begin by defining group actions on A and then exploit these for the study of L. Not all details of our introductory analysis of the module structures of A and L will be used in full for our description of generalized Jacobi identities. We have, however, attempted to present this analysis in its natural general setting, to avoid an unsatisfactory ad hoc collection of merely pragmatic statements.
of a free Lie algebra over an arbitrary commutative ring R with identity 1.Then it turns out that in order to determine all relations of the type mentioned above one has to describe a certain right ideal of the group ring of some symmetric group over R. In fact, our main result will solve the problem by exhibiting an R-basis of this «right ideal of generalized Jacobi identities». Our approach makes use of Witt’s theorem [l,2.3.3] on the embedding of a free Lie algebra L in a free associative algebra A. We begin by defining group actions on A and then exploit these for the study of L. Not all details of our introductory analysis of the module structures of A and L will be used in full for our description of generalized Jacobi identities. We have, however, attempted to present this analysis in its natural general setting, to avoid an unsatisfactory ad hoc collection of merely pragmatic statements.
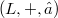 , the following equations hold for arbitrary elements
, the following equations hold for arbitrary elements 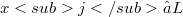 :(Error rendering LaTeX formula) (Error rendering LaTeX formula) In [4,(9a)], Wever already notes that one also has (Error rendering LaTeX formula) and proves some further similar assertions in the same paper [4,Hilfssatz 1]. The aim of this note is, roughly spoken, to determine all relations of this kind.As the relations in question shall hold in any Lie ring, we consider them as relations of free generators
:(Error rendering LaTeX formula) (Error rendering LaTeX formula) In [4,(9a)], Wever already notes that one also has (Error rendering LaTeX formula) and proves some further similar assertions in the same paper [4,Hilfssatz 1]. The aim of this note is, roughly spoken, to determine all relations of this kind.As the relations in question shall hold in any Lie ring, we consider them as relations of free generators 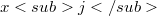 of a free Lie algebra over an arbitrary commutative ring R with identity 1.Then it turns out that in order to determine all relations of the type mentioned above one has to describe a certain right ideal of the group ring of some symmetric group over R. In fact, our main result will solve the problem by exhibiting an R-basis of this «right ideal of generalized Jacobi identities». Our approach makes use of Witt’s theorem [l,2.3.3] on the embedding of a free Lie algebra L in a free associative algebra A. We begin by defining group actions on A and then exploit these for the study of L. Not all details of our introductory analysis of the module structures of A and L will be used in full for our description of generalized Jacobi identities. We have, however, attempted to present this analysis in its natural general setting, to avoid an unsatisfactory ad hoc collection of merely pragmatic statements.
of a free Lie algebra over an arbitrary commutative ring R with identity 1.Then it turns out that in order to determine all relations of the type mentioned above one has to describe a certain right ideal of the group ring of some symmetric group over R. In fact, our main result will solve the problem by exhibiting an R-basis of this «right ideal of generalized Jacobi identities». Our approach makes use of Witt’s theorem [l,2.3.3] on the embedding of a free Lie algebra L in a free associative algebra A. We begin by defining group actions on A and then exploit these for the study of L. Not all details of our introductory analysis of the module structures of A and L will be used in full for our description of generalized Jacobi identities. We have, however, attempted to present this analysis in its natural general setting, to avoid an unsatisfactory ad hoc collection of merely pragmatic statements.DOI Code:
10.1285/i15900932v8n1p111
Full Text: PDF


