Interpolative construction for operator ideals
Abstract
The problem from which this article originated is the following: given an operator 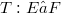 between Banach spaces belonging simultaneously to two operator ideals,
between Banach spaces belonging simultaneously to two operator ideals, 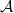 and
and 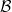 say, when is it possible to find a decomposition
say, when is it possible to find a decomposition 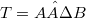 , where
, where 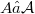 and
and 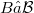 , or at least
, or at least 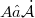 and
and 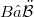 , with
, with 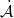 and
and 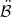 being associated with
being associated with 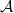 and
and 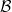 in a specific sense? It was shown by S. Heinrich [2] that such a decomposition is always possible, with
in a specific sense? It was shown by S. Heinrich [2] that such a decomposition is always possible, with 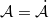 and
and 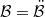 ,if
,if 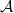 and
and 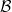 are uniformly closed,
are uniformly closed, 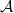 is surjective, and
is surjective, and 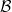 is injective.Heinrich’s arguments are based on a simple interpolation technique which appears to be strongy related to certain general constructions with operator ideals that were successfully applied in a seemingly different context in recent years (ref.[8],[5],and [4]-[7], [1]). We intend to investigate the fundamentals of such constructions and their interpolation-theoretic background in this paper, with emphasis on the impact to the factorization problem.Applications will be given for ideals generated by s-number sequences and to type p and cotype q operators.
is injective.Heinrich’s arguments are based on a simple interpolation technique which appears to be strongy related to certain general constructions with operator ideals that were successfully applied in a seemingly different context in recent years (ref.[8],[5],and [4]-[7], [1]). We intend to investigate the fundamentals of such constructions and their interpolation-theoretic background in this paper, with emphasis on the impact to the factorization problem.Applications will be given for ideals generated by s-number sequences and to type p and cotype q operators.
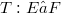 between Banach spaces belonging simultaneously to two operator ideals,
between Banach spaces belonging simultaneously to two operator ideals, 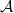 and
and 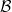 say, when is it possible to find a decomposition
say, when is it possible to find a decomposition 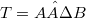 , where
, where 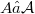 and
and 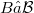 , or at least
, or at least 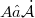 and
and 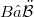 , with
, with 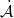 and
and 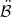 being associated with
being associated with 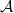 and
and 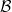 in a specific sense? It was shown by S. Heinrich [2] that such a decomposition is always possible, with
in a specific sense? It was shown by S. Heinrich [2] that such a decomposition is always possible, with 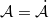 and
and 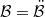 ,if
,if 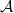 and
and 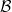 are uniformly closed,
are uniformly closed, 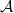 is surjective, and
is surjective, and 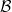 is injective.Heinrich’s arguments are based on a simple interpolation technique which appears to be strongy related to certain general constructions with operator ideals that were successfully applied in a seemingly different context in recent years (ref.[8],[5],and [4]-[7], [1]). We intend to investigate the fundamentals of such constructions and their interpolation-theoretic background in this paper, with emphasis on the impact to the factorization problem.Applications will be given for ideals generated by s-number sequences and to type p and cotype q operators.
is injective.Heinrich’s arguments are based on a simple interpolation technique which appears to be strongy related to certain general constructions with operator ideals that were successfully applied in a seemingly different context in recent years (ref.[8],[5],and [4]-[7], [1]). We intend to investigate the fundamentals of such constructions and their interpolation-theoretic background in this paper, with emphasis on the impact to the factorization problem.Applications will be given for ideals generated by s-number sequences and to type p and cotype q operators.DOI Code:
10.1285/i15900932v8n1p45
Full Text: PDF


