Isoparametric submanifolds
Abstract
In this talk we consider two classes of submanifolds in Euclidean spaces that are characterized by simple local invariants. The first class consists of submanifolds with costant principal curvatures. These are by definition submanifolds 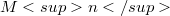 such that for every parallel normal vector field
such that for every parallel normal vector field  along a curve in
along a curve in 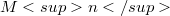 the eigenvalues of the shape operator
the eigenvalues of the shape operator  are constant, see [St] and [0l2]. The second class of submanifolds we will consider consists of isoparametric submainfolds. These are by definition submanifolds
are constant, see [St] and [0l2]. The second class of submanifolds we will consider consists of isoparametric submainfolds. These are by definition submanifolds 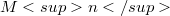 such that the normal bundle is flat and the eigenvalues of the shape operator
such that the normal bundle is flat and the eigenvalues of the shape operator  are constant for every locally defined parallel normal vector field
are constant for every locally defined parallel normal vector field 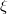 , see [Ha], [CW], [Te] and [PT 2]. It is of course clear that isoparametric submanifolds have constant principal curvatures.
, see [Ha], [CW], [Te] and [PT 2]. It is of course clear that isoparametric submanifolds have constant principal curvatures.
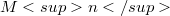 such that for every parallel normal vector field
such that for every parallel normal vector field  along a curve in
along a curve in 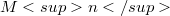 the eigenvalues of the shape operator
the eigenvalues of the shape operator  are constant, see [St] and [0l2]. The second class of submanifolds we will consider consists of isoparametric submainfolds. These are by definition submanifolds
are constant, see [St] and [0l2]. The second class of submanifolds we will consider consists of isoparametric submainfolds. These are by definition submanifolds 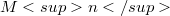 such that the normal bundle is flat and the eigenvalues of the shape operator
such that the normal bundle is flat and the eigenvalues of the shape operator  are constant for every locally defined parallel normal vector field
are constant for every locally defined parallel normal vector field 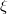 , see [Ha], [CW], [Te] and [PT 2]. It is of course clear that isoparametric submanifolds have constant principal curvatures.
, see [Ha], [CW], [Te] and [PT 2]. It is of course clear that isoparametric submanifolds have constant principal curvatures.DOI Code:
10.1285/i15900932v9supp33
Full Text: PDF


