On semidirect product of semigroups
Abstract
Let X be a subset of a semigroup S. We denote by E(X) the set of idempotent elements Of X.An element a of a semigroup S is called E-inverse if there exists 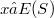 such that
such that 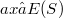 . We note that the definition is not one-sided. Indeed, an a element of a semigroup S is E-inversive if there exists
. We note that the definition is not one-sided. Indeed, an a element of a semigroup S is E-inversive if there exists 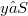 such that
such that 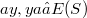 (see [7], [l] p. 98). A semigroup S is called E-inversive if all its elements are E-inversive. This class of semigroups is extensive. All semigroups with a zero and all eventually regular semigroups [2] are E-inversive semigroups.Recently E-inversive semigroups reappeared in a paper by Hall and Munn [3] and in a paper by Mitsch [5]. The special case of E-inversive semigroups with pairwise commuting idempotents, called E-dense, was considered by Margolis and Pin [4]. Let S and T be semigroups, and let
(see [7], [l] p. 98). A semigroup S is called E-inversive if all its elements are E-inversive. This class of semigroups is extensive. All semigroups with a zero and all eventually regular semigroups [2] are E-inversive semigroups.Recently E-inversive semigroups reappeared in a paper by Hall and Munn [3] and in a paper by Mitsch [5]. The special case of E-inversive semigroups with pairwise commuting idempotents, called E-dense, was considered by Margolis and Pin [4]. Let S and T be semigroups, and let 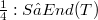 be a homomorphism of S into the endomorphism semigroup of T. If
be a homomorphism of S into the endomorphism semigroup of T. If 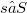 and
and 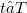 , denote
, denote 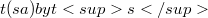 . Thus, if
. Thus, if 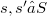 and
and 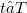 then
then 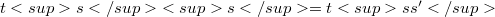 . The semidirect product of S and T ,in that order, with strutture map (Y, consists of the set S x T equipped with the product
. The semidirect product of S and T ,in that order, with strutture map (Y, consists of the set S x T equipped with the product 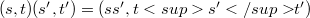 . This product will be denoted by S _{𝛼}T. In this note we determine which semidirect products of semigroups are E-inversive semigroups and E-dense semigroups, respectively. It turns out that the case in which S induces only automorphism on T allows a particularly simple description. In [6], Preston has answered the analous question for regular semigroups and for inverse semigroups. For the terminology and for the definitions of the algebraic theory of semigroups, we refer to [1].
. This product will be denoted by S _{𝛼}T. In this note we determine which semidirect products of semigroups are E-inversive semigroups and E-dense semigroups, respectively. It turns out that the case in which S induces only automorphism on T allows a particularly simple description. In [6], Preston has answered the analous question for regular semigroups and for inverse semigroups. For the terminology and for the definitions of the algebraic theory of semigroups, we refer to [1].
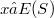 such that
such that 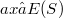 . We note that the definition is not one-sided. Indeed, an a element of a semigroup S is E-inversive if there exists
. We note that the definition is not one-sided. Indeed, an a element of a semigroup S is E-inversive if there exists 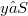 such that
such that 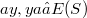 (see [7], [l] p. 98). A semigroup S is called E-inversive if all its elements are E-inversive. This class of semigroups is extensive. All semigroups with a zero and all eventually regular semigroups [2] are E-inversive semigroups.Recently E-inversive semigroups reappeared in a paper by Hall and Munn [3] and in a paper by Mitsch [5]. The special case of E-inversive semigroups with pairwise commuting idempotents, called E-dense, was considered by Margolis and Pin [4]. Let S and T be semigroups, and let
(see [7], [l] p. 98). A semigroup S is called E-inversive if all its elements are E-inversive. This class of semigroups is extensive. All semigroups with a zero and all eventually regular semigroups [2] are E-inversive semigroups.Recently E-inversive semigroups reappeared in a paper by Hall and Munn [3] and in a paper by Mitsch [5]. The special case of E-inversive semigroups with pairwise commuting idempotents, called E-dense, was considered by Margolis and Pin [4]. Let S and T be semigroups, and let 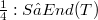 be a homomorphism of S into the endomorphism semigroup of T. If
be a homomorphism of S into the endomorphism semigroup of T. If 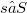 and
and 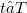 , denote
, denote 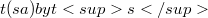 . Thus, if
. Thus, if 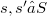 and
and 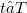 then
then 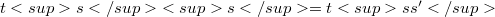 . The semidirect product of S and T ,in that order, with strutture map (Y, consists of the set S x T equipped with the product
. The semidirect product of S and T ,in that order, with strutture map (Y, consists of the set S x T equipped with the product 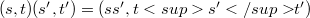 . This product will be denoted by S _{𝛼}T. In this note we determine which semidirect products of semigroups are E-inversive semigroups and E-dense semigroups, respectively. It turns out that the case in which S induces only automorphism on T allows a particularly simple description. In [6], Preston has answered the analous question for regular semigroups and for inverse semigroups. For the terminology and for the definitions of the algebraic theory of semigroups, we refer to [1].
. This product will be denoted by S _{𝛼}T. In this note we determine which semidirect products of semigroups are E-inversive semigroups and E-dense semigroups, respectively. It turns out that the case in which S induces only automorphism on T allows a particularly simple description. In [6], Preston has answered the analous question for regular semigroups and for inverse semigroups. For the terminology and for the definitions of the algebraic theory of semigroups, we refer to [1].DOI Code:
10.1285/i15900932v9n2p189
Full Text: PDF


