Four dimensional symplectic geometry over the field with three elements and a moduli space of Abelian surfaces
Abstract
We study certain combinatorial structures related to the simple group of order 25920. Our viewpoint is to regard this group as 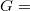
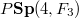 and so we describe these configurations in terms of the symplectic geometry of the four dimensional space over the field with three elements. Because of the isogeny between
and so we describe these configurations in terms of the symplectic geometry of the four dimensional space over the field with three elements. Because of the isogeny between 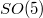 and
and 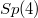 we can also describe these in terms of an inner product space of dimension five over that same field. The study of these configurations goes back to the 19th-century, and we relate our work to that of previous authors. We also discuss a more modern connection: these configurations arise in the theory of the Igusa compactification of the moduli space of principally polarized Abelian surfaces with a level three structure.
we can also describe these in terms of an inner product space of dimension five over that same field. The study of these configurations goes back to the 19th-century, and we relate our work to that of previous authors. We also discuss a more modern connection: these configurations arise in the theory of the Igusa compactification of the moduli space of principally polarized Abelian surfaces with a level three structure.
DOI Code:
10.1285/i15900932v20n1p111
Keywords:
Nsp-spread; Double-six; Orthogonal; Symplectic; Siegel modular variety; Burkhardt quartic
Classification:
20G40; 51E20; 05B25; 11F46
Full Text: PDF


