Topological diagonalizations and Hausdorff dimension
Abstract
The Hausdorff dimension of a product 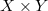 can be strictly greater than that of
can be strictly greater than that of 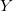 , even when the Hausdorff dimension of
, even when the Hausdorff dimension of 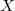 is zero. But when
is zero. But when 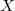 is countable, the Hausdorff dimensions of
is countable, the Hausdorff dimensions of 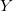 and
and 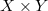 are the same. Diagonalizations of covers define a natural hierarchy of properties which are weaker than "being countable" and stronger than "having Hausdorff dimension zero". Fremlin asked whether it is enough for
are the same. Diagonalizations of covers define a natural hierarchy of properties which are weaker than "being countable" and stronger than "having Hausdorff dimension zero". Fremlin asked whether it is enough for 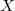 to have the strongest property in this hierarchy (namely, being a
to have the strongest property in this hierarchy (namely, being a 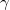 -set) in order to assure that the Hausdorff dimensions of
-set) in order to assure that the Hausdorff dimensions of 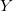 and
and 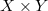 are the same.
are the same.
We give a negative answer: Assuming the Continuum Hypothesis, there exists a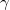 -set
-set 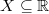 and a set
and a set 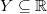 with Hausdorff dimension zero, such that the Hausdorff dimension of
with Hausdorff dimension zero, such that the Hausdorff dimension of 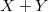 (a Lipschitz image of
(a Lipschitz image of 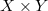 ) is maximal, that is,
) is maximal, that is, 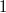 . However, we show that for the notion of a strong
. However, we show that for the notion of a strong 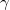 -set the answer is positive. Some related problems remain open.
-set the answer is positive. Some related problems remain open.
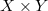 can be strictly greater than that of
can be strictly greater than that of 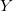 , even when the Hausdorff dimension of
, even when the Hausdorff dimension of 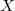 is zero. But when
is zero. But when 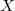 is countable, the Hausdorff dimensions of
is countable, the Hausdorff dimensions of 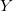 and
and 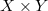 are the same. Diagonalizations of covers define a natural hierarchy of properties which are weaker than "being countable" and stronger than "having Hausdorff dimension zero". Fremlin asked whether it is enough for
are the same. Diagonalizations of covers define a natural hierarchy of properties which are weaker than "being countable" and stronger than "having Hausdorff dimension zero". Fremlin asked whether it is enough for 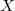 to have the strongest property in this hierarchy (namely, being a
to have the strongest property in this hierarchy (namely, being a 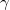 -set) in order to assure that the Hausdorff dimensions of
-set) in order to assure that the Hausdorff dimensions of 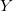 and
and 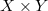 are the same.
are the same. We give a negative answer: Assuming the Continuum Hypothesis, there exists a
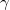 -set
-set 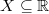 and a set
and a set 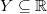 with Hausdorff dimension zero, such that the Hausdorff dimension of
with Hausdorff dimension zero, such that the Hausdorff dimension of 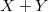 (a Lipschitz image of
(a Lipschitz image of 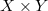 ) is maximal, that is,
) is maximal, that is, 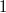 . However, we show that for the notion of a strong
. However, we show that for the notion of a strong 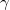 -set the answer is positive. Some related problems remain open.
-set the answer is positive. Some related problems remain open.DOI Code:
10.1285/i15900932v22n2p83
Keywords:
Hausdorff dimension; Gerlits-Nagy $gamma$ property; Galvin-Miller strong $gamma$ property
Classification:
03E75; 37F20; 26A03
Full Text: PDF


