Monochromatic configurations for finite colourings of the plane
Abstract
A strengthened form of Gurevich's conjecture was proved by R.L.Graham ([2],[3]),Which says that for any 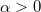 and any pair of non-parallel lines
and any pair of non-parallel lines 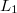 and
and 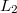 , in any partition of the plane into finitely many classes, some class contains the vertices of a triangle which has area
, in any partition of the plane into finitely many classes, some class contains the vertices of a triangle which has area 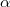 and two sides parallel to the lines
and two sides parallel to the lines 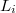 . Later, a shorter proof, using the main idea of Graham, was presented in [1]. Following some questions raised by Graham [2] and by suitable modifications of methods therein, here we establish a similiar in the case of vertices of a trapezium.
. Later, a shorter proof, using the main idea of Graham, was presented in [1]. Following some questions raised by Graham [2] and by suitable modifications of methods therein, here we establish a similiar in the case of vertices of a trapezium.
DOI Code:
10.1285/i15900932v22n1p59
Keywords:
Gurevich's conjecture; Monochromatic configurations
Full Text: PDF


