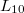 -free
-free 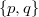 -groups
-groups
Abstract
If 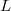 is a lattice, a group is called
is a lattice, a group is called 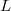 -free if its subgroup lattice has no sublattice isomorphic to
-free if its subgroup lattice has no sublattice isomorphic to 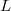 . It is easy to see that
. It is easy to see that 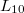 , the subgroup lattice of the dihedral group of order 8, is the largest lattice
, the subgroup lattice of the dihedral group of order 8, is the largest lattice 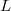 such that every finite
such that every finite 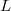 -free
-free 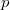 -group is modular. In this paper we continue the study of
-group is modular. In this paper we continue the study of 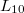 -free groups. We determine all finite
-free groups. We determine all finite 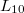 -free
-free 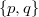 -groups for primes
-groups for primes 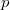 and
and 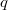 , except those of order
, except those of order 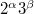 with normal Sylow
with normal Sylow 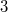 -subgroup
-subgroup
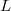 is a lattice, a group is called
is a lattice, a group is called 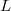 -free if its subgroup lattice has no sublattice isomorphic to
-free if its subgroup lattice has no sublattice isomorphic to 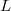 . It is easy to see that
. It is easy to see that 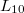 , the subgroup lattice of the dihedral group of order 8, is the largest lattice
, the subgroup lattice of the dihedral group of order 8, is the largest lattice 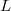 such that every finite
such that every finite 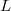 -free
-free 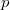 -group is modular. In this paper we continue the study of
-group is modular. In this paper we continue the study of 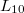 -free groups. We determine all finite
-free groups. We determine all finite 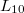 -free
-free 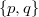 -groups for primes
-groups for primes 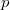 and
and 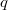 , except those of order
, except those of order 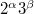 with normal Sylow
with normal Sylow 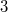 -subgroup
-subgroupDOI Code:
10.1285/i15900932v30n1supplp55
Keywords:
subgroup lattice; sublattice; finite group; modular Sylow subgroup
Full Text: PDF


