On spatial theta-curves with the same 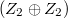 -fold and
-fold and 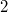 -fold branched covering
-fold branched covering
Abstract
In this note, we study two types of spatial theta-curves having two 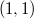 -knotswhose each has two
-knotswhose each has two 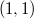 -knotsand a trivial knot or two trivial knots and a
-knotsand a trivial knot or two trivial knots and a 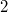 -bridge knot as constituent knots. Weshow that there is a
-bridge knot as constituent knots. Weshow that there is a 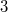 -manifold
-manifold 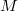 such that
such that 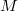 is the
is the 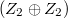 -fold and
-fold and 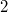 -fold covering of
-fold covering of 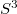 branched over each type of spatial theta-curve. Furthermore, weinvestigate certain relations between the spatial theta-curves and between the closed
branched over each type of spatial theta-curve. Furthermore, weinvestigate certain relations between the spatial theta-curves and between the closed 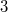 -manifolds which are coverings of
-manifolds which are coverings of 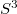 branched over them.
branched over them.
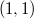 -knotswhose each has two
-knotswhose each has two 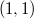 -knotsand a trivial knot or two trivial knots and a
-knotsand a trivial knot or two trivial knots and a 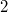 -bridge knot as constituent knots. Weshow that there is a
-bridge knot as constituent knots. Weshow that there is a 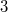 -manifold
-manifold 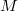 such that
such that 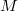 is the
is the 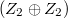 -fold and
-fold and 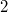 -fold covering of
-fold covering of 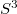 branched over each type of spatial theta-curve. Furthermore, weinvestigate certain relations between the spatial theta-curves and between the closed
branched over each type of spatial theta-curve. Furthermore, weinvestigate certain relations between the spatial theta-curves and between the closed 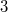 -manifolds which are coverings of
-manifolds which are coverings of 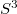 branched over them.
branched over them.DOI Code:
10.1285/i15900932v23n1p111
Keywords:
Spatial theta-curve; Constituent knot; (1; 1)-knot
Classification:
57M12; 57M25
Full Text: PDF


