Locally affine geometries of order 2 where shrinkings are affine expansions
Abstract
Given a locally a affine geometry Γ of order 2 and a flag-transitive subgroup 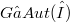 , suppose that the shrinkings of Γ are isomorphic to the a affine expansion of the upper residue of a line of Γ by a homogeneous representation in a 2-group. We shall prove that, under certain hypotheses on the stabilizers Gp and Gl of a point p and a line l, we have G=R{Gp} for a representation group R of
, suppose that the shrinkings of Γ are isomorphic to the a affine expansion of the upper residue of a line of Γ by a homogeneous representation in a 2-group. We shall prove that, under certain hypotheses on the stabilizers Gp and Gl of a point p and a line l, we have G=R{Gp} for a representation group R of 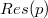 . We also show how to apply this result in the classification of flag-transitive c-extended P- and T-geometries.
. We also show how to apply this result in the classification of flag-transitive c-extended P- and T-geometries.
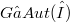 , suppose that the shrinkings of Γ are isomorphic to the a affine expansion of the upper residue of a line of Γ by a homogeneous representation in a 2-group. We shall prove that, under certain hypotheses on the stabilizers Gp and Gl of a point p and a line l, we have G=R{Gp} for a representation group R of
, suppose that the shrinkings of Γ are isomorphic to the a affine expansion of the upper residue of a line of Γ by a homogeneous representation in a 2-group. We shall prove that, under certain hypotheses on the stabilizers Gp and Gl of a point p and a line l, we have G=R{Gp} for a representation group R of 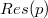 . We also show how to apply this result in the classification of flag-transitive c-extended P- and T-geometries.
. We also show how to apply this result in the classification of flag-transitive c-extended P- and T-geometries.DOI Code:
10.1285/i15900932v24n2p97
Keywords:
Shrinkings; Affine expansions; Representation groups; Sporadic groups
Classification:
51E24; 20D08; 20C34
Full Text: PDF


