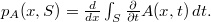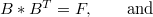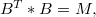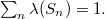Characterization of idempotent 2-copulas
Abstract
A 2-copula 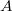 induces a transition probability function
induces a transition probability function 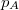 via
via
where
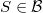 ,
, 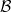 denoting the Lebesgue measurable subsets of
denoting the Lebesgue measurable subsets of![[0,1]](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/ccfcd347d0bf65dc77afe01a3306a96b.png) . We say that a set
. We say that a set 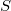 is invariant under
is invariant under 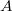 if
if 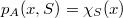 for almost all
for almost all ![x\in [0,1]](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/c628ba2b1047de93f66cb815d986e107.png) ,
, 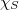 being the characteristic function of
being the characteristic function of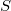 . The sets
. The sets 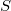 invariant under
invariant under 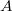 form a sub-
form a sub-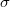 -algebra of theLebesgue measurable sets, which we denote
-algebra of theLebesgue measurable sets, which we denote 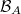 . A set
. A set 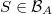 is called an atom if it has positive measure and if for any
is called an atom if it has positive measure and if for any 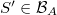 ,
,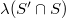 is either
is either 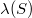 or 0.
or 0.A 2-copula
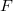 is idempotent if
is idempotent if 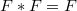 . Here
. Here  denotes the product defined in [1]. Idempotent 2-copulas are classified and characterized asfollows:
denotes the product defined in [1]. Idempotent 2-copulas are classified and characterized asfollows:(i) An idempotent
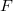 is said to be nonatomic if
is said to be nonatomic if 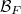 contains noatoms. If
contains noatoms. If 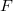 is a nonatomic idempotent, then it is the product of a leftinvertible copula and its transpose. That is, there exists a copula
is a nonatomic idempotent, then it is the product of a leftinvertible copula and its transpose. That is, there exists a copula 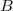 such that
such that where
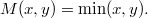
(ii) An idempotent
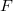 is said to be totally atomic if there exist essentiallydisjoint atoms
is said to be totally atomic if there exist essentiallydisjoint atoms 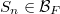 with
withIf
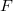 is a totally atomic idempotent, then it is conjugate to an ordinal sumof copies of the product copula. That is, there exists a copula
is a totally atomic idempotent, then it is conjugate to an ordinal sumof copies of the product copula. That is, there exists a copula 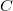 satisfying
satisfying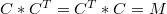 and a partition
and a partition 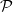 of
of ![[0,1]](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/ccfcd347d0bf65dc77afe01a3306a96b.png) such that
such that\begin{equation}F=C*(\oplus _{\cal P}F_k)*C^T \end{equation} where eachcomponent
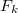 in the ordinal sum is the product copula
in the ordinal sum is the product copula 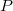 .
.(iii) An idempotent
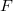 is said to be atomic (but not totally atomic) if
is said to be atomic (but not totally atomic) if 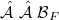 contains atoms but the sum of the measures of a maximal collection ofessentially disjoint atoms is strictly less than 1. In this mixed case, thereexists a copula
contains atoms but the sum of the measures of a maximal collection ofessentially disjoint atoms is strictly less than 1. In this mixed case, thereexists a copula 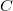 invertible with respect to
invertible with respect to 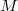 and a partition
and a partition 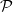 of
of![[0,1]](http://siba-ese.unisalento.it/plugins/generic/latexRender/cache/ccfcd347d0bf65dc77afe01a3306a96b.png) for which (1) holds, with
for which (1) holds, with 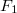 being a nonatomic idempotent copula andwith
being a nonatomic idempotent copula andwith 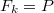 for
for 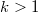 .
.Some of the immediate consequences of this characterization are discussed.
DOI Code:
10.1285/i15900932v30n1p147
Keywords:
copula; idempotent; star product
copula; idempotent; star product
Classification:
60G07; 60J05; 60J25
Full Text: PDF