On Norden-Walker 4-manifolds
Abstract
A Walker 4-manifold is a semi-Riemannian manifold 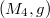 of neutral signature, which admits a field of parallel null 2-plane. The main purpose of the present paper is to study almost Norden structures on 4-dimensional Walker manifolds with respect to a proper and opposite almost complex structures. We discuss sequently the problem of integrability, Kähler (holomorphic), isotropic quasi-Kähler conditions for these structures. The curvature properties for Norden-Walker metrics is also investigated. Also, we give counterexamples to Goldberg's conjecture in the case of neutral signature.
of neutral signature, which admits a field of parallel null 2-plane. The main purpose of the present paper is to study almost Norden structures on 4-dimensional Walker manifolds with respect to a proper and opposite almost complex structures. We discuss sequently the problem of integrability, Kähler (holomorphic), isotropic quasi-Kähler conditions for these structures. The curvature properties for Norden-Walker metrics is also investigated. Also, we give counterexamples to Goldberg's conjecture in the case of neutral signature.
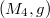 of neutral signature, which admits a field of parallel null 2-plane. The main purpose of the present paper is to study almost Norden structures on 4-dimensional Walker manifolds with respect to a proper and opposite almost complex structures. We discuss sequently the problem of integrability, Kähler (holomorphic), isotropic quasi-Kähler conditions for these structures. The curvature properties for Norden-Walker metrics is also investigated. Also, we give counterexamples to Goldberg's conjecture in the case of neutral signature.
of neutral signature, which admits a field of parallel null 2-plane. The main purpose of the present paper is to study almost Norden structures on 4-dimensional Walker manifolds with respect to a proper and opposite almost complex structures. We discuss sequently the problem of integrability, Kähler (holomorphic), isotropic quasi-Kähler conditions for these structures. The curvature properties for Norden-Walker metrics is also investigated. Also, we give counterexamples to Goldberg's conjecture in the case of neutral signature.DOI Code:
10.1285/i15900932v30n1p111
Keywords:
Walker 4-manifolds; Proper almost complex structure; Opposite almost complex structure; Norden metrics; Holomorphic metrics; Goldberg conjecture
Walker 4-manifolds; Proper almost complex structure; Opposite almost complex structure; Norden metrics; Holomorphic metrics; Goldberg conjecture
Classification:
53C50; 53B30
Full Text: PDF


