A note on some homology spheres which are 2-fold coverings of inequivalent knots
Abstract
We construct a family of closed 3--manifolds 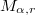 , which are homeomorphic to the Brieskorn homology spheres
, which are homeomorphic to the Brieskorn homology spheres 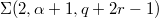 , where
, where 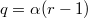 and both
and both 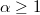 and
and 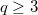 are odd. We show that
are odd. We show that 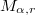 can be represented as 2--fold covering of the 3--sphere branched over two inequivalent knots. Our proofs follow immediately from two different symmetries of a genus 2 Heegaard diagram of
can be represented as 2--fold covering of the 3--sphere branched over two inequivalent knots. Our proofs follow immediately from two different symmetries of a genus 2 Heegaard diagram of 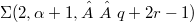 , and generalize analogous results proved in [BGM], [IK], [SIK] and [T].
, and generalize analogous results proved in [BGM], [IK], [SIK] and [T].
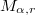 , which are homeomorphic to the Brieskorn homology spheres
, which are homeomorphic to the Brieskorn homology spheres 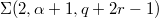 , where
, where 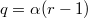 and both
and both 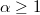 and
and 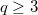 are odd. We show that
are odd. We show that 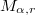 can be represented as 2--fold covering of the 3--sphere branched over two inequivalent knots. Our proofs follow immediately from two different symmetries of a genus 2 Heegaard diagram of
can be represented as 2--fold covering of the 3--sphere branched over two inequivalent knots. Our proofs follow immediately from two different symmetries of a genus 2 Heegaard diagram of 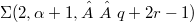 , and generalize analogous results proved in [BGM], [IK], [SIK] and [T].
, and generalize analogous results proved in [BGM], [IK], [SIK] and [T].DOI Code:
10.1285/i15900932v30n1p41
Keywords:
3–manifold; branched covering; orbifold; fundamental group; homology 3–sphere; (1, 1)-knot; torus knot
3–manifold; branched covering; orbifold; fundamental group; homology 3–sphere; (1, 1)-knot; torus knot
Classification:
57M05; 57M12; 57R65
Full Text: PDF


