Limiting behaviour of moving average processes under 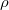 -mixing assumption
-mixing assumption
Abstract
Let 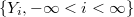 be a doubly infinite sequence of identically distributed
be a doubly infinite sequence of identically distributed 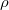 -mixing random variables,
-mixing random variables, 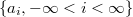 an absolutely summable sequence of real numbers. In this paper, we prove the complete convergence and Marcinkiewicz-Zygmund strong law of large numbers for the partial sums of the moving average processes
an absolutely summable sequence of real numbers. In this paper, we prove the complete convergence and Marcinkiewicz-Zygmund strong law of large numbers for the partial sums of the moving average processes 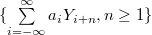 .
.
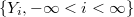 be a doubly infinite sequence of identically distributed
be a doubly infinite sequence of identically distributed 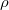 -mixing random variables,
-mixing random variables, 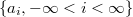 an absolutely summable sequence of real numbers. In this paper, we prove the complete convergence and Marcinkiewicz-Zygmund strong law of large numbers for the partial sums of the moving average processes
an absolutely summable sequence of real numbers. In this paper, we prove the complete convergence and Marcinkiewicz-Zygmund strong law of large numbers for the partial sums of the moving average processes 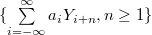 .
.DOI Code:
10.1285/i15900932v30n1p17
Keywords:
moving average; Ï?-mixing; complete convergence; Marcinkiewicz-Zygmund strong laws of large numbers
moving average; Ï?-mixing; complete convergence; Marcinkiewicz-Zygmund strong laws of large numbers
Classification:
60F15
Full Text: PDF


