Vector Space Partitions and Designs Part I-Basic Theory
Abstract
This article, written in two parts, concerns partitions of finite vectorspaces of dimension 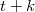 by one subspace of dimension
by one subspace of dimension 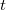 (the `focus') andthe remaining subspaces of dimension
(the `focus') andthe remaining subspaces of dimension 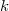 ; a `focal-spread of type
; a `focal-spread of type 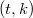 '.Focal-spreads of type
'.Focal-spreads of type 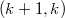 also produce
also produce 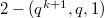 -designs, \and various other double and triple-spreads. There are three differentmethods given to construct focal-spreads, one of which is due toBeutelspacher. In this Part I, we shall also provide a coordinate method fortheir construction analogous to matrix spread sets for translation planes. InPart II, we shall give a new construction that we term "going up," whichalso allows a specification of certain subplanes of the focal-spread.Additive focal-spreads are shown to be equivalent to additive partialspreads. Various applications are given relative to additive partial spreadsand semifield planes admitting exotic subplanes. Finally, also in Part II, ,the developments of focal-spreads may be applied to construct a variety ofnew subgeometry partitions of projective spaces.
-designs, \and various other double and triple-spreads. There are three differentmethods given to construct focal-spreads, one of which is due toBeutelspacher. In this Part I, we shall also provide a coordinate method fortheir construction analogous to matrix spread sets for translation planes. InPart II, we shall give a new construction that we term "going up," whichalso allows a specification of certain subplanes of the focal-spread.Additive focal-spreads are shown to be equivalent to additive partialspreads. Various applications are given relative to additive partial spreadsand semifield planes admitting exotic subplanes. Finally, also in Part II, ,the developments of focal-spreads may be applied to construct a variety ofnew subgeometry partitions of projective spaces.
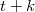 by one subspace of dimension
by one subspace of dimension 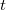 (the `focus') andthe remaining subspaces of dimension
(the `focus') andthe remaining subspaces of dimension 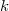 ; a `focal-spread of type
; a `focal-spread of type 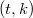 '.Focal-spreads of type
'.Focal-spreads of type 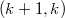 also produce
also produce 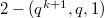 -designs, \and various other double and triple-spreads. There are three differentmethods given to construct focal-spreads, one of which is due toBeutelspacher. In this Part I, we shall also provide a coordinate method fortheir construction analogous to matrix spread sets for translation planes. InPart II, we shall give a new construction that we term "going up," whichalso allows a specification of certain subplanes of the focal-spread.Additive focal-spreads are shown to be equivalent to additive partialspreads. Various applications are given relative to additive partial spreadsand semifield planes admitting exotic subplanes. Finally, also in Part II, ,the developments of focal-spreads may be applied to construct a variety ofnew subgeometry partitions of projective spaces.
-designs, \and various other double and triple-spreads. There are three differentmethods given to construct focal-spreads, one of which is due toBeutelspacher. In this Part I, we shall also provide a coordinate method fortheir construction analogous to matrix spread sets for translation planes. InPart II, we shall give a new construction that we term "going up," whichalso allows a specification of certain subplanes of the focal-spread.Additive focal-spreads are shown to be equivalent to additive partialspreads. Various applications are given relative to additive partial spreadsand semifield planes admitting exotic subplanes. Finally, also in Part II, ,the developments of focal-spreads may be applied to construct a variety ofnew subgeometry partitions of projective spaces.DOI Code:
10.1285/i15900932v29n2p165
Keywords:
vector space partition; designs; focal-spread
vector space partition; designs; focal-spread
Full Text: PDF


