Generalized 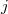-planes

Abstract

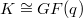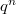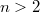We construct and study a class of translation planes with kernel , order , and . These planes generalize the 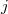-planes discovered by Johnson, Pomareda and Wilke in [14]. We show these planes are actually 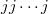-planes. Hence, most of the results obtained in this article are on 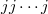-planes. In fact, our study shows that these planes are either nearfield or new.

An infinite class of nearfield 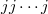-planes is shown to exist, and a finite set of sporadic non-Andr\'e 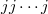-planes is presented.