Invariants on primary abelian groups and a problem of Nunke
Abstract
If  is an arbitrary abelian
is an arbitrary abelian 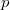 -group, an invariant
-group, an invariant 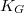 is defined which measures how closely
is defined which measures how closely  resembles a direct sum of cyclic groups. This invariant consists of a class of finite sets of regular cardinals, and is inductively constructed using filtrations of various subgroups of
resembles a direct sum of cyclic groups. This invariant consists of a class of finite sets of regular cardinals, and is inductively constructed using filtrations of various subgroups of  ;
; 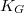 can also be considered to be a measure of the presence of non-zero elements of infinite height in
can also be considered to be a measure of the presence of non-zero elements of infinite height in  . This construction is particularly useful when the group has final rank less than the smallest weakly Mahlo cardinal; and in this case,
. This construction is particularly useful when the group has final rank less than the smallest weakly Mahlo cardinal; and in this case,  is a direct sum of cyclics iff
is a direct sum of cyclics iff 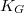 is empty. These deliberations are then used to place several of the most significant results relating to direct sums of cyclics into a significantly broader context. For example,
is empty. These deliberations are then used to place several of the most significant results relating to direct sums of cyclics into a significantly broader context. For example,  is shown to be almost a direct sum of cyclics iff every set in
is shown to be almost a direct sum of cyclics iff every set in 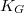 has at least two elements. Finally,
has at least two elements. Finally, 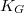 is used to give a more complete and concrete answer to a classical problem of Nunke, which asks when the torsion product of two abelian
is used to give a more complete and concrete answer to a classical problem of Nunke, which asks when the torsion product of two abelian 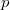 -groups is a direct sum of cyclics.
-groups is a direct sum of cyclics.
primary abelian groups; direct sums of cyclics; invariants; filtrations; torsion product; almost direct sums of cyclics
Full Text: PDF


