Geometric structures arising from generalized 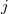 -planes
-planes
Abstract
We study translation planes constructed by Andr\'e net replacement on 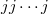 -planes and derivation on
-planes and derivation on 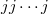 -planes. Then, we get to the conclusion that the family of non-Andr\'e
-planes. Then, we get to the conclusion that the family of non-Andr\'e 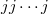 -planes is new, and thus so are their replaced and derived planes.
-planes is new, and thus so are their replaced and derived planes.
We also study a new way to construct translation planes by putting together two `halves' of planes that belong to two different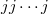 -planes. We show examples of planes of small order constructed this way.
-planes. We show examples of planes of small order constructed this way.
Finally, we prove that using regular hyperbolic covers,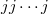 -planes induce partitions of Segre varieties by Veronesians (sometimes called flat flocks)
-planes induce partitions of Segre varieties by Veronesians (sometimes called flat flocks)
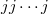 -planes and derivation on
-planes and derivation on 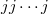 -planes. Then, we get to the conclusion that the family of non-Andr\'e
-planes. Then, we get to the conclusion that the family of non-Andr\'e 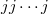 -planes is new, and thus so are their replaced and derived planes.
-planes is new, and thus so are their replaced and derived planes.We also study a new way to construct translation planes by putting together two `halves' of planes that belong to two different
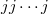 -planes. We show examples of planes of small order constructed this way.
-planes. We show examples of planes of small order constructed this way.Finally, we prove that using regular hyperbolic covers,
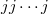 -planes induce partitions of Segre varieties by Veronesians (sometimes called flat flocks)
-planes induce partitions of Segre varieties by Veronesians (sometimes called flat flocks)DOI Code:
10.1285/i15900932v29n2p1
Keywords:
Translation planes; Andrè nets; derivable nets; glat flocks; generalized j-planes
Translation planes; Andrè nets; derivable nets; glat flocks; generalized j-planes
Full Text: PDF


