Lifting the solutions of a Toeplitz type equation; the semigroup case(Error rendering LaTeX formula)
Abstract
A Toeplitz operator with respect to a contractive representation 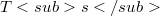 of an abelian semigroup
of an abelian semigroup 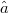 in a Hilbert space H is an operator
in a Hilbert space H is an operator 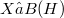 such that(Error rendering LaTeX formula) for all
such that(Error rendering LaTeX formula) for all 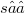 . We show that if
. We show that if 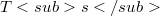 has a minimal isometric dilation
has a minimal isometric dilation 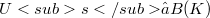 , then Toeplitz operators can be obtained in a unique way as compressions of operators
, then Toeplitz operators can be obtained in a unique way as compressions of operators 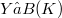 , called Toeplitz symbols, such that(Error rendering LaTeX formula). This approach to lifting the Toeplitz equation(Error rendering LaTeX formula) is shown to be unitarily equivalent to the one proposed by Muhly in 1972. We use our approach to extend to this case a number of theorems about classical Toeplitz operators and, finally, we show that some classes of well-known operators like Wiener-Hopf operators Toeplitz operators in
, called Toeplitz symbols, such that(Error rendering LaTeX formula). This approach to lifting the Toeplitz equation(Error rendering LaTeX formula) is shown to be unitarily equivalent to the one proposed by Muhly in 1972. We use our approach to extend to this case a number of theorems about classical Toeplitz operators and, finally, we show that some classes of well-known operators like Wiener-Hopf operators Toeplitz operators in 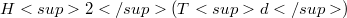 or Toeplitz operators in the sense of Murphy fall within the class studied in this paper. The main objective of this paper is to provide a general framework that, we hope, will be useful in order to extend to wider classes of operators some of the more recent and deep advances in the theory of Toeplitz operators.
or Toeplitz operators in the sense of Murphy fall within the class studied in this paper. The main objective of this paper is to provide a general framework that, we hope, will be useful in order to extend to wider classes of operators some of the more recent and deep advances in the theory of Toeplitz operators.
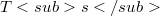 of an abelian semigroup
of an abelian semigroup 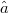 in a Hilbert space H is an operator
in a Hilbert space H is an operator 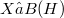 such that(Error rendering LaTeX formula) for all
such that(Error rendering LaTeX formula) for all 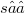 . We show that if
. We show that if 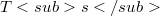 has a minimal isometric dilation
has a minimal isometric dilation 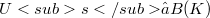 , then Toeplitz operators can be obtained in a unique way as compressions of operators
, then Toeplitz operators can be obtained in a unique way as compressions of operators 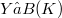 , called Toeplitz symbols, such that(Error rendering LaTeX formula). This approach to lifting the Toeplitz equation(Error rendering LaTeX formula) is shown to be unitarily equivalent to the one proposed by Muhly in 1972. We use our approach to extend to this case a number of theorems about classical Toeplitz operators and, finally, we show that some classes of well-known operators like Wiener-Hopf operators Toeplitz operators in
, called Toeplitz symbols, such that(Error rendering LaTeX formula). This approach to lifting the Toeplitz equation(Error rendering LaTeX formula) is shown to be unitarily equivalent to the one proposed by Muhly in 1972. We use our approach to extend to this case a number of theorems about classical Toeplitz operators and, finally, we show that some classes of well-known operators like Wiener-Hopf operators Toeplitz operators in 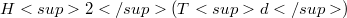 or Toeplitz operators in the sense of Murphy fall within the class studied in this paper. The main objective of this paper is to provide a general framework that, we hope, will be useful in order to extend to wider classes of operators some of the more recent and deep advances in the theory of Toeplitz operators.
or Toeplitz operators in the sense of Murphy fall within the class studied in this paper. The main objective of this paper is to provide a general framework that, we hope, will be useful in order to extend to wider classes of operators some of the more recent and deep advances in the theory of Toeplitz operators.DOI Code:
10.1285/i15900932v25n1p231
Keywords:
Toeplitz operators; Weiner-Hopf operators; Operator semigroups; Minimal isometric dilation
Classification:
47B35; 47A10; 47A20; 47A53; 47A62
Full Text: PDF


