Pointwise multipliers on L1 and related spaces
Abstract
We consider completely continuous and weakly compact multiplication operators on certain classical function spaces, more precisely on Lebesgue spaces 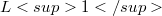 on spaces
on spaces 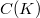 of continuous functions on a compact Hausdorff space K,and on the Hardy space
of continuous functions on a compact Hausdorff space K,and on the Hardy space 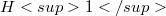 . We will describe such operators in terms of their defining symbols. Our characterizations extend corresponding results known from the literature. In any case, our results reveal the severe restrictions on the symbols of multiplication operators necessary to ensure complete continuity or weak compactness. The apparent simplicity of the obtained descriptions belie the deep and beautiful functional analytic principles that underlie them.
. We will describe such operators in terms of their defining symbols. Our characterizations extend corresponding results known from the literature. In any case, our results reveal the severe restrictions on the symbols of multiplication operators necessary to ensure complete continuity or weak compactness. The apparent simplicity of the obtained descriptions belie the deep and beautiful functional analytic principles that underlie them.
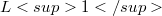 on spaces
on spaces 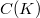 of continuous functions on a compact Hausdorff space K,and on the Hardy space
of continuous functions on a compact Hausdorff space K,and on the Hardy space 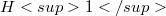 . We will describe such operators in terms of their defining symbols. Our characterizations extend corresponding results known from the literature. In any case, our results reveal the severe restrictions on the symbols of multiplication operators necessary to ensure complete continuity or weak compactness. The apparent simplicity of the obtained descriptions belie the deep and beautiful functional analytic principles that underlie them.
. We will describe such operators in terms of their defining symbols. Our characterizations extend corresponding results known from the literature. In any case, our results reveal the severe restrictions on the symbols of multiplication operators necessary to ensure complete continuity or weak compactness. The apparent simplicity of the obtained descriptions belie the deep and beautiful functional analytic principles that underlie them.DOI Code:
10.1285/i15900932v25n1p221
Keywords:
Multiplication operators; $L1$; $C(K)$; $H1$; Weak compactness; Complete continuity
Classification:
47B38; 47B07; 28A99
Full Text: PDF


