Existence and uniqueness theorem for Frenet frame supercurves
Abstract
In the first part of this paper,using the Banach Grassmann algebra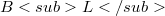 
given by Rogers in her paper [10],a new scalar product and a new
definition of the orthogonality are introduced on the 
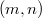-dimensional total supereuclidean space 
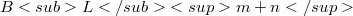. Using the GH∈fty functions given by Rogers in [10], the new definitions of the supercurve, of the supersmooth supercurve, of the supersmooth supercurve in general position and of the Frenet frame associated to a supersmooth supercurve in general position are given. In second part of this paper, using the classical results described in [9], the new existence and uniqueness theorem for some supercurves which admit Frenet frame is proved.
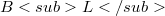given by Rogers in her paper [10],a new scalar product and a new
definition of the orthogonality are introduced on the 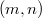-dimensional total supereuclidean space 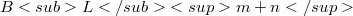. Using the GH∈fty functions given by Rogers in [10], the new definitions of the supercurve, of the supersmooth supercurve, of the supersmooth supercurve in general position and of the Frenet frame associated to a supersmooth supercurve in general position are given. In second part of this paper, using the classical results described in [9], the new existence and uniqueness theorem for some supercurves which admit Frenet frame is proved.DOI Code:
10.1285/i15900932v24n1p143
Keywords:
$(m, n)$-dimensional total supereuclidean space ${BL}m+n$; The $(m, n)$-dimensional supereuclidean space ${BL}m+n$; The $GH∞$ functions; Supersmooth supercurve; Supersmooth supercurve in general position; Frenet frame associated to a supersmooth supercurve; Frenet formulas for the supersmooth supercurve
Classification:
58A50
Full Text: PDF
