Art galleries with k-guarded guards
Abstract
The k-guarde art galllery problem asks for the minimum number of k-guarded point guards that can collectively monitor a simple polygon with n vertices. A guard is k-guarded if it can see k other guards. For k = 0, this problem is equivalent to the classical art gallery problem of Klee. For k 0 1, a tight bound of 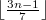 was shown recently by Micheal and Pinviu and independently, by Zilinski. In this paper, we settle the problem for every
was shown recently by Micheal and Pinviu and independently, by Zilinski. In this paper, we settle the problem for every 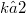 and show that
and show that 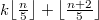 k-guarded guards are always sufficient and sometimes necessary to guard a simple polygon with n vertices.
k-guarded guards are always sufficient and sometimes necessary to guard a simple polygon with n vertices.
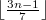 was shown recently by Micheal and Pinviu and independently, by Zilinski. In this paper, we settle the problem for every
was shown recently by Micheal and Pinviu and independently, by Zilinski. In this paper, we settle the problem for every 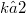 and show that
and show that 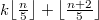 k-guarded guards are always sufficient and sometimes necessary to guard a simple polygon with n vertices.
k-guarded guards are always sufficient and sometimes necessary to guard a simple polygon with n vertices.DOI Code:
10.1285/i15900932v24n1p111
Keywords:
The art gallery problem; Guarded guards
Classification:
52C99; 05C90
Full Text: PDF


