Introduction
Abstract
En
In this paper, some basic properties (recurrence relations,asymptotic expansion, series representation and others) are derived for the new function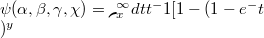 , which covers certain well-known special functions for particular choices of the parameteres
, which covers certain well-known special functions for particular choices of the parameteres 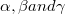 . For example, for
. For example, for 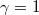 and
and 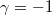 ,
, 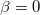 one obtains respectively
one obtains respectively 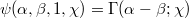 and
and 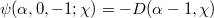 ,where(Error rendering LaTeX formula) is the complementary incomplete Gamma function and
,where(Error rendering LaTeX formula) is the complementary incomplete Gamma function and 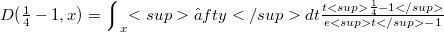 is a function of Debye type.The function
is a function of Debye type.The function 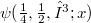 has been introduce by us in order to find a class of exact solutions for nonlinear wave equations of the Klein-Gordon type
has been introduce by us in order to find a class of exact solutions for nonlinear wave equations of the Klein-Gordon type 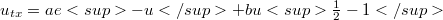 , where
, where 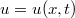 and a, b are constants.
and a, b are constants.
In this paper, some basic properties (recurrence relations,asymptotic expansion, series representation and others) are derived for the new function
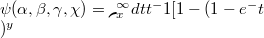 , which covers certain well-known special functions for particular choices of the parameteres
, which covers certain well-known special functions for particular choices of the parameteres 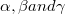 . For example, for
. For example, for 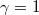 and
and 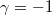 ,
, 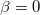 one obtains respectively
one obtains respectively 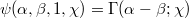 and
and 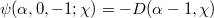 ,where(Error rendering LaTeX formula) is the complementary incomplete Gamma function and
,where(Error rendering LaTeX formula) is the complementary incomplete Gamma function and 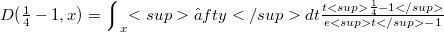 is a function of Debye type.The function
is a function of Debye type.The function 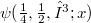 has been introduce by us in order to find a class of exact solutions for nonlinear wave equations of the Klein-Gordon type
has been introduce by us in order to find a class of exact solutions for nonlinear wave equations of the Klein-Gordon type 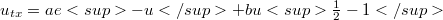 , where
, where 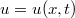 and a, b are constants.
and a, b are constants.DOI Code:
¦
Full Text: PDF


