Introduzione
Abstract
En
The jet spaces of maps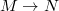 and of the sections of a bundle
and of the sections of a bundle 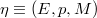 are considered,analysing their vector and affine structures. An intrinsic characterization of second order jet spaces is given. When the bundle η is affine or linear,further results are given. Some interesting maps concerning jet spaces are defined. The k-Lie derivable bundles are introduced and the k-Lie derivative is defined: particular cases are connections
are considered,analysing their vector and affine structures. An intrinsic characterization of second order jet spaces is given. When the bundle η is affine or linear,further results are given. Some interesting maps concerning jet spaces are defined. The k-Lie derivable bundles are introduced and the k-Lie derivative is defined: particular cases are connections 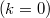 , usual Lie-derivaties
, usual Lie-derivaties 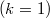 and Lie-derivaties of geometrical objects. Connections on a bundle are analysed and related with the affine structures of jet spaces and tangent spaces.
and Lie-derivaties of geometrical objects. Connections on a bundle are analysed and related with the affine structures of jet spaces and tangent spaces.
The jet spaces of maps
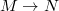 and of the sections of a bundle
and of the sections of a bundle 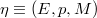 are considered,analysing their vector and affine structures. An intrinsic characterization of second order jet spaces is given. When the bundle η is affine or linear,further results are given. Some interesting maps concerning jet spaces are defined. The k-Lie derivable bundles are introduced and the k-Lie derivative is defined: particular cases are connections
are considered,analysing their vector and affine structures. An intrinsic characterization of second order jet spaces is given. When the bundle η is affine or linear,further results are given. Some interesting maps concerning jet spaces are defined. The k-Lie derivable bundles are introduced and the k-Lie derivative is defined: particular cases are connections 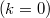 , usual Lie-derivaties
, usual Lie-derivaties 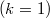 and Lie-derivaties of geometrical objects. Connections on a bundle are analysed and related with the affine structures of jet spaces and tangent spaces.
and Lie-derivaties of geometrical objects. Connections on a bundle are analysed and related with the affine structures of jet spaces and tangent spaces.DOI Code:
§
Full Text: PDF


