Introduzione
Abstract
En
Given a set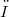 , a finitely additive probability measure
, a finitely additive probability measure 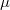 on
on 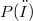 is considered. Let
is considered. Let 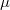 be "strongly" non-atomic: we prove that there exists a sequence
be "strongly" non-atomic: we prove that there exists a sequence 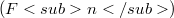 of subsets of
of subsets of 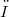 (mutually disjoint and with
(mutually disjoint and with 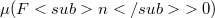 ) whose union has measure equal to an arbitrarily given Øø╝ (with
) whose union has measure equal to an arbitrarily given Øø╝ (with 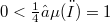 ) and such that
) and such that 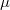 is countably additive on them. As a simple corollary, the following property (well-known for countably additive measures)is deduced: the range of
is countably additive on them. As a simple corollary, the following property (well-known for countably additive measures)is deduced: the range of 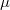 is the whole interval [0,1]. In the last part of the paper, some aspects of a decomposition theorem by B. De Finetti (for an arbitrary
is the whole interval [0,1]. In the last part of the paper, some aspects of a decomposition theorem by B. De Finetti (for an arbitrary 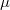 ) are deepened.
) are deepened.
Given a set
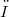 , a finitely additive probability measure
, a finitely additive probability measure 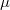 on
on 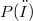 is considered. Let
is considered. Let 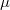 be "strongly" non-atomic: we prove that there exists a sequence
be "strongly" non-atomic: we prove that there exists a sequence 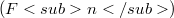 of subsets of
of subsets of 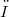 (mutually disjoint and with
(mutually disjoint and with 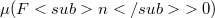 ) whose union has measure equal to an arbitrarily given Øø╝ (with
) whose union has measure equal to an arbitrarily given Øø╝ (with 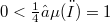 ) and such that
) and such that 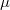 is countably additive on them. As a simple corollary, the following property (well-known for countably additive measures)is deduced: the range of
is countably additive on them. As a simple corollary, the following property (well-known for countably additive measures)is deduced: the range of 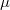 is the whole interval [0,1]. In the last part of the paper, some aspects of a decomposition theorem by B. De Finetti (for an arbitrary
is the whole interval [0,1]. In the last part of the paper, some aspects of a decomposition theorem by B. De Finetti (for an arbitrary 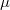 ) are deepened.
) are deepened.DOI Code:
¦
Full Text: PDF


