An extreme example concerning factorization products on the Schwartz space 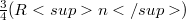
Klaus Detlef Kürsten, Martin Läuter
Abstract
We construct linear operators S, T mapping the Schwartz space 𝕾 into its dual 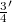 , such that any operator
, such that any operator 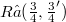 may be obtained as factorization product
may be obtained as factorization product 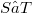 . More precisely, given
. More precisely, given 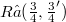 , there exists a Hilbert space
, there exists a Hilbert space 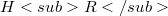 such that
such that 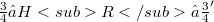 , the embeddings
, the embeddings 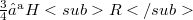 and
and 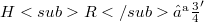 are continuous,
are continuous, 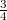 is dense in
is dense in 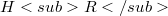 ,
, 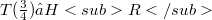 , and S has a continuous extension
, and S has a continuous extension 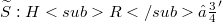 such that
such that 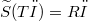 for all φ ∈ 𝕾.
for all φ ∈ 𝕾.
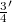 , such that any operator
, such that any operator 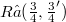 may be obtained as factorization product
may be obtained as factorization product 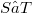 . More precisely, given
. More precisely, given 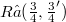 , there exists a Hilbert space
, there exists a Hilbert space 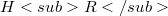 such that
such that 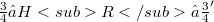 , the embeddings
, the embeddings 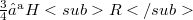 and
and 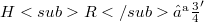 are continuous,
are continuous, 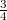 is dense in
is dense in 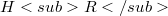 ,
, 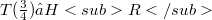 , and S has a continuous extension
, and S has a continuous extension 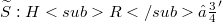 such that
such that 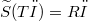 for all φ ∈ 𝕾.
for all φ ∈ 𝕾.